Student Seminar Talks

Past Seminars

• Fall 2022

  Thursday, November 10th, 2022

  

  Counting From Infinity

  Yitang Zhang and the Twin Prime Conjecture, A Film by George Csicsery

  In April 2013, a lecturer at the University of New Hampshire submitted a paper to the Annals of Mathematics. Within weeks work spread: a little-known mathematician, with no permanent job, working in complete isolation, had made an important breakthrough toward solving the Twin Prime Conjecture. Yitang Zhang’s techniques for bounding the gaps between primes soon led to rapid progress by the Polymath Group, and a further innovation by James Maynard.

  Thursday, November 3rd, 2022

  Professor Kim Plofker - Union College

  

  Convergence: Understanding what happens to sequences and series in ancient Greek and Indian mathematics

  Nowadays most of us encounter the concepts of convergence and divergence when we study limits and series in calculus. But mathematicians and philosophers were interested in them for many centuries before the development of calculus. We'll look at some of the discoveries, pitfalls and paradoxes concerning convergence in the mathematical traditions of ancient Greece and India.

  Professor emeritus William Zwicker, Union College, will be presenting - Fair division of graphs and of tangled cakes, Ayumi Igarashi(a) and William S. Zwicker(b)

  Union's newest building, Mainly Hall(c), will be shared by the three most venerable and prestigious academic departments: Mathematics, Philosophy, and Physics. The dean wishes to assign the new offices to faculty in these three departments, in such a way that

  • no department prefers the set of offices assigned to a different department to those allocated to itself . . .
  • . . . and members of any one department can walk among offices assigned to faculty in that department without needing to walk past offices of faculty in other departments.

  • Does such an assignment always exist?
  • Fair Division studies how to share some common resource among several agents in a way that is "fair." In Fair Division of Graphsby introducing tangles – an even newer context for fair division. A tangle (see examples below) is a continuous mathematical space built by gluing together several copies of the unit interval [0, 1]. Our theorems then transfer results from the continuous world of tangles to the discrete world of graphs.

  

  (a) University of Tokyo, Japan

  (b) Murat Sertel Center for Advanced Economic Studies, Istanbul Bilgi University; Union College Mathematics Department, Schenectady NY, USA

  (c) So named because most of Mainly Hall is taken up by a huge, empty atrium – wasted space meant to impress visiting prospective students and their parents.

  

  Thursday, October 20, 2022

  Professor Phanuel Mariano will be presenting - The Hot Spots Problem

  Consider a perfectly insulated 1-dimensional rod, or a 2-dimensional plate, or better yet, a 3-dimensional room. Perfectly insulated means that heat cannot escape this room. The Hot Spots Problem asks about what happens to the location of the ``hot spots'' and ``cold spots'' of this insulated body over a long period of time. To understand this problem we will introduce the equation that describes the evolution of heat over time. Moreover, we will discuss what is known (and not known) about this problem. We end the talk by discussing the connection between the Hot Spots Problem and Probability theory. In particular, this connection will be through a theory of random particles called Brownian motion.

  Thursday, September 15, 2022

  Professor Jeff Jauregui will be presenting - Measure & Size

  Volumes of familiar shapes like cubes, spheres, and cylinders are easy to calculate, with formulas that have been known for thousands of years. But how can we find (or even define) the volumes of shapes which are much more complicated, possibly with jagged edges and infinitely many holes? Measure theory is all about studying such volumes (and, in two dimensions, areas) and has applications to integration, probability, physics, and even finance. This talk is a casual introduction to the subject. Along the way, we'll encounter exotic objects such as the Cantor Set, Sierpiński Carpet, and Menger Sponge.

  Thursday, September 22, 2022

  Professor emeritus Julius Barbanel - Union College

  The Ancient Greeks and Irrational Numbers: discovery, crisis, resolution

  Pythagoras and his followers (who lived and worked about 2500 years ago) thought it obvious that any two line segments are commensurable, or, in other words, that given any two line segments, there is some third line segment that measures each. This assumption turns out to be equivalent to the statement "all real numbers are rational." Many ancient Greek geometric proofs used this assumption. When it was discovered that this assumption is false, it caused a mathematical crisis. We shall explore the reasons why the Pythagoreans made this commensurability assumption, the discovery that it is false, the ensuing mathematical crisis, and the resolution of this crisis by Eudoxus.

• Spring 2022

  Thursday, Sept 29th

  

  Professor Holley Friedlander, Dickinson College will be presenting - Arithmetic of Apollonian Circle Packings

  The concept of an Apollonian packing dates to Hellenistic Greece when astronomer Apollonius of Perga discovered the following theorem: Given an arrangement of three circles such that every pair is mutually tangent, there are precisely two circles tangent to all three.

  Start with four mutually tangent circles. In the space between any three, add the (unique) circle tangent to all three. Repeat this process of successively adding new circles to every new threesome of circles ad infinitum and one obtains an infinite configuration of circles known as an Apollonian circle packing. If each of the four initial circles has integer curvature, then amazingly all the circles in the packing must have integer curvature. For such a packing, there are many questions a number theorist might ask. For example, are there infinitely many circles with prime curvature? In this talk, we introduce and discuss the arithmetic of Apollonian circle packings.

  Thursday, May 26th, 2022 - 12:45-1:55pm - Bailey 207

  

  Professor Samuel Taylor - Temple University

  Growth in groups via linear algebra

  Finite groups are often studied using basic combinatorics and number theory, as in a first course in Abstract Algebra. For infinite groups, however, many of these techniques are unavailable. Since so many infinite groups play an important role in geometry and topology, different methods need to be developed for their study. In this talk, I’ll introduce the growth of a group, which is perhaps the most basic notion of `size’ when the group is infinite. As we shall see, for certain classes of groups, growth can be studied using properties of directed graphs and basic linear algebra. Our focus will be on some elementary (but important!) examples that require absolutely no previous background in group theory.

  Friday, May 13

  In deference to the annual Steinmetz Symposium, Friday, May 13, there will not be a separate math seminar this week. Instead, we encourage you to attend the talks and to read the posters prepared by students in the math department (as well as many others!).

  Thursday, May 19th, 2022

  12:30pm pizza & beverages in Bailey 204

  12:55pm Seminar - in Bailey 207

  Design – 3D Print – Calculate: Student Created 3D Printed Solids of Revolution

  Profs. Lucy Oremland and Csilla Szabo, Skidmore College

  In mathematics, it is often necessary to build, visualize, and manipulate complex multi-dimensional structures. Instructors and students must become makers - through drawing, simulating, and crafting - in order to engage deeply with key concepts. In this talk we present a solids of revolution making activity for Calculus II (Integral Calculus). As part of the activity, students designed and 3D printed volumes of solids of revolution using our college’s maker space.

  We will demonstrate the steps required to create a digital solid of revolution using free online tools, Desmos and Fusion360. If you would like to follow along with the demonstration, please bring a laptop and complete the steps below to get free access to Fusion360.

  • Create an Autodesk account (Free access for 1 year for students and educators.) https://www.autodesk.com/education/edu-software/overview?sorting=featured&filters=individual
  • Access Fusion360 online at https://fusion.online.autodesk.com/ or download to your computer.

  • Design – 3D Print – Calculate: Student Created 3D Printed Solids of Revolution

    Profs. Lucy Oremland and Csilla Szabo, Skidmore College

  May 5, 2022 - 4:30-7:00pm - OLIN 115

  What is Actuarial Science, and What Career Opportunities Does It Offer?

  

  John W Robinson, President-Elect, Society of Actuaries

  Introduction: John W Robinson (FAA MAAA FCA) is currently President and Chief Actuary of Robinson Associates, LLC. He has over thirty-five years’ experience as a practicing actuary, including in state government. Originally from Jamaica, John received his B.S. in Mathematics from the University of the West Indies, and has M.S. degrees in Statistics from both the University of Delaware and Florida State University. John has served as President of the International Association of Black Actuaries, and on the SOA Board of Directors for several years. He will become the first Black President of the SOA when he assumes the office on October 22, 2022.

  Our talk:

  The Mathematics Department, Economics Department, Center for Data Analytics, and Becker Career Center are delighted to jointly sponsor a presentation by John W Robinson, recently elected as President-Elect of the Society of Actuaries (SOA). The SOA is the world’s largest actuarial professional organization, with over 32,000 members. In this two-part presentation, John will first explain what actuarial science is and what specific disciplines are involved. After a catered meal break, John will discuss his own career as an actuary, as well as the broader career opportunities that this discipline offers. Feel free to attend either or both parts, depending on interest. This session builds upon the recently approved new minor in Financial and Actuarial Mathematics, and will be organized as follows:

  • 4:30 – 5:30pm Part I What is Actuarial Science?

  • 5:30 – 6:00pm Catered meal break

  • 6:00 – 7:00pm Part II Careers in Actuarial Science

  Thursday, April 21st 2022 - 12:55pm - Bailey 207

  Richard Guy’s Strong Law of Small Numbers and How Not to Make Friends

  Professor Hanson Smith - University of Connecticut

  In this talk we will work through a number of examples from Richard Guy's wonderful paper The Strong Law of Small Numbers. The main theorem is, “You can't tell by looking.” Following Guy, we will prove this by intimidation. Audience participation, questioning, and guessing is highly encouraged. We'll conclude the talk with an exciting application to web comics.

  2+1=3 is prime.

  2⋅3+1=7 is prime.

  2⋅3⋅5+1=31 is prime.

  2⋅3⋅5⋅7+1=211 is prime.

  2⋅3⋅5⋅7⋅11+1=2311 is prime.

  Does it continue?

  Thursday, April 14th 2022 - 12:55pm - Bailey 207

  Understanding and Addressing Complexity in Problem-Solving

  Professor Roger Hoerl - Union College

  Problem-solving is commonly applied in virtually all disciplines. The Hungarian mathematician George Polya wrote a classic text on problem-solving in 1945 that has sold over one million copies. One might argue that statistics as a discipline developed because of unsolved problems in other disciplines, such as conducting the US Census, public health, and agriculture. Unfortunately, much of the literature on problem-solving focuses narrowly on technical complexity and ignores other critical aspects of complexity that must be considered in real problems, such as organizational or political complexity.

  In this talk, we will briefly discuss the development of the theory of problem-solving, beginning with Polya. We will then discuss broader aspects of problem-solving complexity that need to be considered for success, noting the critical but often overlooked impact of complexity in properly defining the problem. We will apply these principles to a couple of major problems facing our society today, and offer some thoughts on how to approach complex problems in general.

  Pizza lunch at 12:30 in Bailey 204 for those students attending the seminar

  Thursday, April 7th 2022 - 12:55pm

  Geometric Constructions in Number Theory

  Professor Jeff Hatley - Union College

  Thursday, April 7th, 12:55pm, BAIL-207

  One of the most satisfying aspects of mathematics is finding bridges between seemingly-disparate fields. These sorts of connections abound between number theory and geometry -- in fact, there is an entire field, called "arithmetic geometry," which studies this sort of thing.

  In this talk, we will explore one big (geometric) idea and the insight it provides for two very classical number theory problems. We will begin with a problem of interest to the ancient Greeks, and we will end on a modern, wide-open conjecture whose solution is worth $1 million.

  The prerequisites for this talk are high school algebra and an affinity for pictures.

• Fall 2021

  Thursday, November 18th, 2021

  12:30pm - 1:45pm pizza & beverages in Bailey 204

  Study Break - Math Majors/Minors Meet and Greet

  In lieu of a talk this week, please stop by Bailey 204 this Thursday from 12:30-1:45 for a pizza study break. Math majors and minors (and other math students), please come and mingle with each other, and math faculty as well, as we all prepare for finals.

  Thursday, November 11th, 2021

  12:30pm pizza & beverages in Bailey 204

  12:55pm Seminar - in Bailey 207

  Some Unusual Dice and their Connections to Voting

  Professor Davide Cervone, Union College

  We are all familiar with the property that, for numbers, if $a > b$ and $b > c$, then $a > c$, and it is reasonable to expect that this property would hold in other situations where one thing "beats" another in some way. It turns out that this is not always the case, however. For example, in voting, it is possible to have candidate $A$ be preferred to candidate $B$ by a majority of voters, and $B$ preferred to $C$ by a majority, but also have $C$ preferred to $A$ by a majority of voters! This was described by the Marquis de Condorcet at the end of the 18th century, and is referred to as a Condorcet cycle, and it makes it hard to decide who should be the winner in an election that contains such a cycle. Similar cycles can be found in other situations as well. For example, it is possible to produce a set of three dice where the first beats the second more than half the time, the second beats the third more often than not, while the third beats the first more than 50% of the time. Such "non-transitive dice" have a close connection to the voting situation, and understanding one can help understand the other. In this talk, we illustrate the connection between voting and non-transitive dice, explore how they work with longer cycles, and generalize these cycles to ones involving the comparison of more than two dice (or candidates) at a time.

  Friday, November 5th

  4:00pm pizza & beverages in Bailey 204

  4:30pm Seminar - in Bailey 207

  Solving probability using differential (in)equations

  Professor Joe P. Chen, Colgate University

  In calculus or analysis we learned the notion of convergence, $\lim_{n\to\infty} x_n =x$. It would be even better if we can quantify the rate of convergence, namely, how fast does $|x_n-x|$ decay to $0$ as $n \to \infty$? Exponential? Or as a power law? Now translate these questions in the setting of your favorite probabilistic model (random walks, Langevin diffusion, etc. Or you can use last week's talk as an example). All you know is that the model converges to a stationary distribution as time $n\to\infty$. But how fast does it converge? And since the model might be idealized, can you come up with a real-world algorithm that approximately samples this stationary distribution? And how good is the approximation? One answer to this question can be obtained through the analysis of a first-order-in-time differential inequality called the "entropy inequality." After sketching the basic properties of relative entropy, I will explain the structure of the entropy inequality, and illustrate its use in recent research in math and computer science.

  Thursday, October 28th, 2021

  12:30pm pizza & beverages in Bailey 204

  12:55pm Seminar - in Bailey 207

  Solving Differential Equations with Probability

  Professor Phanuel De Andrade, Union College

  In this talk I will discuss how one can solve second order differential equations using the notion of Brownian motion, which is a mathematical model for the random movement of a particle. It was first observed by Robert Brown in 1827 while looking at pollen grains through a microscope. Since then, Brownian motion has been used in many applications to physics, finance and other branches of math. In 1944, Shizuo Kakutani was the first to use a probabilistic approach to solve a differential equation with a boundary condition. We will use this approach to solve a simple boundary value problem that one could encounter in an elementary differential equations class.

  Thursday, October 21st, 2021

  12:30pm pizza & beverages in Bailey 204

  12:55pm Seminar - in Bailey 207

  The Joy of Abstraction, presented by professor emeritus Kimmo Rosenthal, Union College

  “The imagination is the only genius. It is intrepid and eager and the extreme of its achievement lies in abstraction.” Wallace Stevens.

  It may seem incongruous for the epigraph to a mathematics talk to be from one of the great American poets. However, while the ubiquity and utility of mathematics is widely acknowledged, its aesthetic appeal is much less so. In this day and age when relevance, applicability, and connections with other disciplines are touted as paramount, is there still a place for purely abstract mathematics viewed more as an intellectual art form? Can the old dictum “art for art’s sake” be replaced by “math for math’s sake”?

  Abstraction has always appealed to me and indeed guided me. Yet, in some quarters it can provoke outright hostility. We shall take a brief historical tour of mathematical abstraction from the set theory of Georg Cantor (called a “corrupter of youth”) to the mysterious emergence of Nicolas Bourbaki (the famous mathematician who never existed), and finally category theory, which earned the epithet of “abstract nonsense”.

  There will be a gentle introduction to category theory accessible to anyone taking Math 199, including consideration of the question: can we talk about sets without mentioning elements?

  Thursday, October 14th, 2021

  12:30pm pizza & beverages in Bailey 204

  12:55pm Seminar - in Bailey 207

  Connecting cluster algebras to continued fractions and snake graphs

  Professor Michelle Rabideau - University of Hartford

  

  In many areas of mathematics, it is often beneficial to represent objects graphically or numerically. In this talk, we study the class of commutative rings called cluster algebras and their elements called cluster variables. We will focus on one particular characteristic of a cluster variable and study it by considering graphs of square tiles called snake graphs and using numerical tools called continued fractions. The talk will emphasize how mathematicians often change strategies when the current method becomes too abstract, too tedious or too time consuming to be reasonable.

  Thursday, October 7th, 2021

  12:30pm pizza & beverages in Bailey 204

  12:55pm Seminar - in Bailey 207

  Ultrametrics, strange geometries, and p-adic numbers

  Professor Jeffrey Hatley - Union College

  Different settings call for different ways of measuring distance. I can measure my daily commute by the length of road I travel, or I could measure the distance between my home and Union "as the crow flies." In the city, we might describe distances in terms of blocks -- routes constructed from straight-line paths and right-angle turns. You can even measure distance in more abstract, non-physical settings, such as the distance between you and your second cousin. In this light-hearted talk we'll discuss various notions of distance and explore some of the surprising consequences for "basic" geometric notions, such as what circles and triangles look like. We'll end by explaining why the usual geometry that everyone learns in high school is the strangest of them all.

  Pre-requisites: If you know what a circle is, this talk is for you!

  Thursday, September 30th

  12:30pm pizza & beverages in Bailey 204

  12:55pm Seminar - in Bailey 207

  Come to hear about student research!

  Josh DaRosa (ME '22), Zekai Hu (MT '22), and Zhebin Yin (MTCS '22)

  Interested in learning about students' research over the summer / academic year? Josh will present data analysis within PIV fluid dynamics research and PIV measurements of heterogeneous canopies. Zekai (Kai) will present predicting one year survival rate for heart failure patients and COVID-19 patients with heart disease. Zhebin (Irene) will present classification of lung cancer circulating tumor cells in liquid biopsy using deep learning.

  Thursday, September 23rd

  12:30pm pizza & beverages in Bailey 204

  12:55pm Seminar - Note: due to construction, will be in Bailey 201

  How To Cut A Cake, presented by Union College professor emeritus Julius Barbanel

  Suppose that you and I are given a cake that we wish to divide between the two of us. We may value pieces of cake differently. For example, maybe I like the chocolate filling best, but you like the icing best, so a piece of cake that I value as half the cake, you might value as a third of the cake. What would constitute a “good” division of the cake? We shall consider two sorts of criteria, namely “fairness” and “efficiency”. Fairness involves such questions as “Did I get at least half?” or “Did I get at least as much as you?” Efficiency involves
  questions such as “Is this the best way to divide the cake or is there a way to divide the cake that would make each of us happier?” We will see that there are interesting mathematical ideas and revealing geometric pictures associated with these issues. We will also consider what happens when we wish to divide the cake among more than two people.

• Spring 2021

  Greg Malen, Union College, "High-Dimensional Holeyominoes and Hyperbolic Polyforms"

  A polyomino is a finite ``rook-connected'' subset of squares on an infinite chessboard, which one can imagine is constructed by taking individual square tiles and gluing them together along their edges. In this talk, I will be considering extremal properties of these structures with respect to the requirement that a fixed number of squares is arranged such that their edges bound a maximal number of holes. These ``holeyominoes'' tend towards beautiful symmetries and efficient geometric properties. Building on earlier results with squares in 2-dimensional Euclidean space, I will present new asymptotic bounds for the maximum number of holes which can be bounded by $n$ $d$-dimensional cubes in $d$-dimensional Euclidean space. Furthermore, we will look at on-going efforts to find similar results in the hyperbolic plane for subsets of a $\{p,q\}$-tiling, where $q$ regular $p$-gons meet at every vertex.

  Date/time: Thursday, May 27th at 1:20pm-2:15pm

  Location: Zoom ID: https://union.zoom.us/j/92591304428

  Mary Annese ACAS, CPCU, MAAA, to present “An Introduction to the Actuarial Profession”

  An introduction to a promising career in what has been touted as one of the nation’s top ranked professions because of its employability, career growth, high-paying salaries, and work-life balance.

  Date/time: Thursday, May 6th at 1:20pm-2:15pm

  Location: Zoom ID: https://union.zoom.us/j/92591304428

  What you will learn:

  • What an Actuary is
  • What Actuaries do
  • How to become an Actuary
  • What the Casualty Actuarial Society is
  • Why this is an attractive career
  • Your next steps

  Who should attend?

  • Undergraduate students majoring in actuarial science, math, statistics, business, or other related fields
  • Undecided undergraduate students with an interest in math, statistics, business, or other related fields.
  • Go to: CASstudentcentral.org and register to become a student member. It’s free and provides you access to a wealth of tips, tools and resources.

  Emily Hoopes-Boyd from Kent State University

  Date/time: Thursday, April 15th at 1:20pm-2:15pm

  Location: Zoom ID: https://union.zoom.us/j/92591304428

  Title: The Images of Polynomials Evaluated over Matrices

  Abstract: A version of the L’vov-Kaplansky conjecture states that the image of a multilinear polynomial evaluated over matrices, with entries from the complex numbers, is a vector space. This statement has been proven only for the case of 2×2 matrices, but many partial results have been proven within the last decade. We will consider this problem in a slightly different context; rather than taking the matrix entries to be from the complex numbers, we will consider matrices over an algebraically closed skew field, which we will denote by $K$. We will show that the image of any multilinear polynomial with coefficients from $K$, evaluated over $M_m(K)$, is $M_m(K)$. We will also prove that any matrix in $M_m(K)$ may be written as the sum of three or fewer elements from the image of any generalized polynomial. In particular, the image of the polynomial $xy-yx$ has some special properties over a variety of matrix rings, including the ring of matrices over the complex numbers.

• Winter 2020

  Wednesday, January 29th

  12:30pm pizza & beverages in Bailey 204

  12:55pm Seminar will be in Bailey 207

  Please see flyers posted in Bailey Hall for title and abstract

  Friday, January 31st

  4:00pm light refreshments in Bailey 204

  4:15pm Seminar will be in Bailey 207

  Please see flyers posted in Bailey Hall for title and abstract

  Thursday, Jan 23rd

  Making Our Mark, Women in Mathematics, at Union and Beyond

  In conjunction with our celebration of the 50th anniversary of co-education at Union College, we invite you all to a special celebration of women in mathematics in our upcoming math seminar. We will hear from Professor Susan Niefield about her experience as a mathematician and as the first woman who joined the math department faculty at Union. We will then briefly introduce some professional organizations that focus on making the mathematical community more inclusive. In particular, members of The Association for Women in Mathematics Chapter at Union will share their stories and talk about their events and resources. Finally, we will watch a short film "Journeys of Women in Mathematics", that shows the difficulties and triumphs of three women mathematicians from three different continents: Neela Nataraj from India, Aminatou Pecha from Cameroon, and Carolina Araujo from Brazil.

  Thursday, January 16th - Union College welcomes:

  Mary Annese ACAS, CPCU, MAAA, to present “An Introduction to the Actuarial Profession”

  An introduction to a promising career in what has been touted as one of the nation’s top ranked professions because of its employability, career growth, high-paying salaries, and work-life balance.

  What you will learn:

  • What an Actuary is
  • What Actuaries do
  • How to become an Actuary
  • What the Casualty Actuarial Society is
  • Why this is an attractive career
  • Your next steps

  Who should attend?

  • Undergraduate students majoring in actuarial science, math, statistics, business, or other related fields
  • Undecided undergraduate students with an interest in math, statistics, business, or other related fields.

  Go to: CASstudentcentral.org and register to become a student member. It’s free and provides you access to a wealth of tips, tools and resources.

• Fall 2019

  Injectivity of polynomial maps and multistationarity in reaction networks

  Professor Casian Pantea, West Virginia University

  Friday, Nov 08th - 1:00pm – BAIL 207

  The capacity of biochemical reaction networks to operate at different steady states is crucial in important biological processes like cell division, differentiation, or apoptosis. In this talk we attack the question “when can a certain reaction network admit two or more positive steady states?”, i.e., when can the network be multistationary? This boils down to a difficult question about solutions of some high-dimensional polynomial systems, further complicated by the lack of information on coefficient values. However, it turns out that a lot can be said on multistationarity of reaction networks by studying the injectivity of the corresponding polynomial maps. We will survey some classical and some new results on the topic, and illustrate them using relevant biological examples.

  The Strange New Universe of Hyperbolic Geometry

  Professor Ellen Gasparovic, Union College

  Friday, Nov 1st - 1:00pm – BAIL 201

  

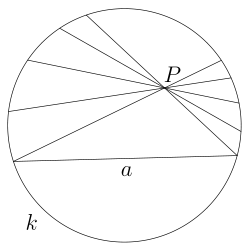
  The fifth postulate in Euclid's Elements states that, in a plane, given a line l and a point P not on l, there is exactly one line through P that is parallel to l. Although this is an axiom in Euclidean geometry, what happens when you don't assume that the so-called "parallel postulate" holds? The answer is that beautiful non-Euclidean geometries emerge, such as that of the hyperbolic plane (what mathematician Janos Bolyai referred to as a "strange new universe"). In this talk, we will learn about what it means for lines to be "parallel" or "ultra-parallel" in this strange new setting, with an eye toward classifying all distance-preserving transformations using the Klein disk model for the hyperbolic plane.

  The Congruent Number Problem

  Professor Jeff Hatley, Union College

  Thursday, Oct 24th - 1:00pm – BAIL 207

  The Congruent Number Problem asks the following simple-sounding question: which rational numbers occur as the area of a right triangle with sides of rational length? For example, the familiar (3,4,5) right triangle has area 6, so 6 is a congruent number; but Fermat showed in the year 1640 that 1 is not a congruent number. Our investigation of this question will lead to a surprising and beautiful interaction between algebra and geometry, bringing us to the forefront of modern number theory and a math problem with a $1 Million prize.

  Joint Math-CS Student Seminar

  DeepFake the Menace?

  Dr. Siwei Lyu

  University at Albany

  Thursday, Oct 17th - 1:00pm – VART 204

  The advancements of AI technology, in particular, deep generative models, have enabled the creation of fake images, audios and videos in ways that have not been possible before. Such fake videos, commonly known as the DeepFakes, are eroding our trust to digital media and causing serious ethical, legal, social, and financial consequences. In this talk, I will briefly review the technologies behind the creation of DeepFakes, and then introduce current detection methods of such fake videos and measures that can obstruct the generation of DeepFakes, as well as general technical aspects to combat DeepFakes.

  The Interface of Science, Engineering, and Statistics

  Professor Roger Hoerl - Union College

  Thursday, Oct 10th, 1:00pm, BAIL-207

  In essence, science expands our understanding of the fundamental workings of the natural world. Engineering, on the other hand, takes our knowledge of the natural world and attempts to apply it in some way that benefits society. Real engineering applications typically venture beyond the boundaries of our scientific knowledge, resulting in uncertainty, and with some degree of "trial and error" required. Google's experiences with self-driving cars would be an obvious example. At its best, statistics accelerates science and engineering by efficiently filling in the gaps in our scientific theory using empirical data analysis. This seminar will illustrate these concepts using a case study from the author's previous experience as a statistical intern at the DuPont Company.

  Connecting STE with M

  Professor Robert Rogers - SUNY Fredonia - 2019-2020 "MAA Seaway Section Distinguished Lecturer"

  Thursday, Oct 3rd, 1:00pm, VART-204

  Theoretic chemistry, internet security, kidney stone treatment, airfoil design; what connects these seemingly diverse science, technology, and engineering topics? This talk will explore the mathematics behind these topics. Furthermore, the mathematical topics required to understand these applications only involve drawing, counting, numbers, some geometry, and some imagination.

  Thursday, September 26th, 1:00pm, Bailey 207

  Featuring: Student talks

  Meichai Chen (Class of 2020), Herschel Norwitz (Class 2021), and

  Mushan Zhong (Class of 2020)

  **************************************

  Meichai Chen ('20)

  Weak Orders and Utility Functions
  A weak order is a complete and transitive order on a set X, whose elements we refer to as preferences. In this talk, we will explore the connections between weak orders and utility functions. We will then briefly discuss how weak orders and utility functions arise in expected utility theory and prospect theory, and conclude with a short description of how these concepts are used in a study regarding stereotype threat.

  Herschel Norwitz ('21)

  Distinguishing between Forced and Natural oscillations on the Power Grid

  Oscillations are always occurring on the grid. The two forms of oscillations that occur are natural and forced. Observing natural oscillations can tell the health of the system, unfortunately forced oscillations occur that don't effect the health of the system but can make it appear as though the system is unhealthy. In this research a dynamometer and a DC motor were used to inject a forced oscillations into the outlet. Then using Matlab and a python program measurements are taken from an outlet so see if it is not only possible to observe the oscillations but distinguish them.
  
  Mushan Zhong ('20)
  Use of Nonlinear Models in Analyzing Experiments with Both Mixture and Process Variables
  When conducting statistics experiments; In most cases we can experiment with different combinations of variables without restrictions. While there are some other cases in which the experimental variables are ingredients, and must sum to 100%. These are called mixture variables. Our research focused on how to approach problems with both process and also mixture variables. We tested different models to see how well they could fit a given set of data, as well as how well they predicted new data. The objective was to develop models that can be applied to smaller data sets, which would allow researchers to run smaller, cheaper, and faster experiments.

  Featuring: Student summer research

  Dan Resnick (class 2021)

  Sam Kemp (class 2021)

  Friday, September 20th, 1:00pm, Bailey 207

  Dan Resnick (class 2021)

  Stellar Wind Collisions: Thin Shell Geometry
  I will be talking about the theory behind the stellar wind problem and the assumptions/setup to where we started working. I will discuss the methods we used and where we stopped on the problem, and where we plan to go forward with the project.

  Sam Kemp (class 2021)
  Simulation of Forces Between Inclusions on a Lipid Bilayer
  A program was written in C++ to simulate the forces between two inclusions on a lipid bilayer using the finite element method. This was first done using Dirichlet boundary conditions and then with mixed boundary conditions at the edge of the inclusions.

• Spring 2019

  The Historical Roots of Gödel’s Theorems

  Professor Andrea Pedeferri - Philosophy Department @ Union College

  Tuesday, May 28th, 1:00pm, Bailey 207

  At the beginning of “On formally undecidable propositions of Principia Mathematica and related systems” Gödel writes: “The development of mathematics toward greater precision has led [...] to the formalization of large tracts of it, so that one can prove any theorem using nothing but a few mechanical rules.” In just few sentences Gödel summarizes a century of key developments in mathematics that made that period one of the most exciting and optimistic for the discipline. As Hilbert wrote in 1925 and in 1930 “we are all convinced that [...] in mathematics there is no ignorabimus”, “We must know. We will know”.

  Then comes 1931. Gödel writes: “One might therefore conjecture that these axioms and rules of inference are sufficient to decide any mathematical question [...]. It will be shown below that this is not the case [...]. The precise analysis of this curious situation leads to surprising results concerning consistency proofs for formal systems.” The impact of Gödel’s results was immense.

  In my talk I will follow the main developments of mathematics highlighted by Gödel in order to show how they are crucial to understand the impact and the reach of Gödel’s theorems and to fully appreciate their dramatic but revolutionary nature.

  Rationalizable Voting Rules and the S-Correspondence

  Professor Ashley Piggins, Department of Economics, National University of Ireland, Galway (joint work with Conal Duddy, Department of Economics, University College, Cork)

  Tuesday, May 21st, 4:00pm, Bailey 207

  Perhaps the most important feature in Kenneth Arrow’s famous “Impossibility Theorem” (which helped him earn a Nobel prize in Economics) is IIA – the Independence of Irrelevant Alternatives condition on voting rules, aka social choice. We introduce a related but new social choice property, the S-independence condition. We characterize the “S-correspondences” – those social choice rules that satisfy S-independence along with three more standard axioms: strong Pareto optimality, neutrality and anonymity. This class is closely related to the S-rules of Bossert and Suzumura (2008a, J. Econ. Theory 138, 311-320). S-independence can be justified by a new rationalizability argument that shows it is equivalent to assuming IIA in a somewhat different framework.

  The History of Fermat's Last Theorem

  Professor Ravi Ramakrishna, Cornell University

  Thursday, May 16th, 1:00pm, Bailey 207

  In 1994, Wiles, assisted by Taylor, finally settled the 340-year-old question of Fermat's Last Theorem. In this talk I will give some of the history of this problem, with particular focus on events of 1847 and the 1980-90s. I'll then talk a little about developments off the last 25 years in the subject.

  This talk is NOT aimed at faculty in number theory. It is intended for undergrads that like math, but have not taken many upper level courses.

  Mathematical Modeling in Computational Neuroscience

  Paulina Volosov, Rensselaer Polytechnic Institute

  Thursday, May 2nd, 1:00pm, Bailey 207, with lunch at 12:30pm in Bailey 204

  Computational neuroscience is a field of active research for applied mathematicians. The brain has been actively studied since the second half of the 19th century, but there are still an endless number of unanswered questions about how and why the brain works the way it does.
  
  This presentation will give a basic introduction to some of the questions asked in neuroscience and show how a mathematical model can be built and used to shed light on this complicated biological system. Namely, how can a mathematician attempt to learn about the structure of the brain and networks of neurons? What is it that a mathematical model tries to accomplish? And why is this useful?

  Who Discovered Integral Calculus?

  Professor Emeritus Julius Barbanel, Union College

  Thursday, April 25th, 1:00pm, Bailey 207, with lunch at 12:30pm in Bailey 204

  Isaac Newton and Gottfried Leibniz (both working in the late 17th and early 18th centuries CE) are generally considered to be the inventors of calculus. We will argue in this talk that part of the credit for this discovery should be given to the ancient Greek mathematician Archimedes (who worked in the 3rd century BCE). Archimedes pursued two lines of research involving areas and volumes. These approaches, known as the Method of Exhaustion and the Mechanical Method, can be viewed as early examples of ideas that we think of as being part of integral calculus. We will focus on Archimedes’ Method of Exhaustion.

  Presenting Mathematics - an open discussion

  Professor Leila Khatami and Professor Jue Wang, Union College

  Thursday, April 18th, 1:00pm, Bailey 207, with lunch at 12:30pm in Bailey 204

  As Steinmetz symposium approaches, many students are contemplating their presentations and are thinking about ways to make an engaging presentations to effectively share their work with fellow students, family members, and professors. Even those who are not presenting this year, will most probably present their work in the future. In this seminar, we will talk about some of the characteristics of a good mathematics presentation, as well as some of common missteps to avoid. As part of the discussion, we will also watch and analyze a short sample presentation.

  Math, ECBE, Physics and Astronomy joint seminar

  Thursday April 11, 2019, during common hour in Karp 005

  Towards Cyber-Physical Electrical Power Systems: where the laws of nature and the rules of algorithms collide!

  Luigi Vanfretti
  Electrical, Computer, and Systems Engineering, RPI

  Electrical power networks are undergoing unprecedented changes. On one hand, the adoption of distributed energy resources (DER) and renewable energy sources (RES), both of which have a large degree of variability in small time-scales, puts challenges to the traditional, historical-and-experience-based design and operation of electrical power networks. On the other hand, digitization and automation, opens opportunities for a more carbon neutral electrical energy system by helping to harmonize these new energy sources with the rest of the power grid, not without also bringing along the potential threats of the cyber world. This talk aims to give an overview of these challenges, and to present different research efforts conducted by the presenter to address how to transform today’s electrical grid into a cyber-physical power system. This includes the development of an experimental facility to conduct, real-time hardware-in-the-loop simulation experiments of power networks with “cyber” assets. This approach allows to characterize how the interaction of systems governed by the laws of nature will interact with engineered systems governed by rules of algorithms. Finally, with the rise of electrification in transport, and in particular aircraft, and the rise of more autonomous machines, the talk will also discuss the need for development of a new course on modeling and simulation for cyber-physical systems (CPS) and the teaching approach adopted which brings a “digital” toolbox and know-how to the next generation of electrical engineers that will have to increasingly deal with complex CPS.

• Winter 2019

  The Spectacular Spectral Theory

  Ehssan Khanmohammadi, Union College

  Thursday, March 7th, 1:00pm, Bailey 207, with reception at 12:30pm in Bailey 204

  Do you know the reason for the collapse of the Tacoma Narrows Bridge in 1940? Have you ever wondered about the mathematical idea behind Google’s page ranking and Netflix’s movie recommendation? Do you know why scientists believe that distant stars are largely composed of hydrogen?
  
  This talk is an invitation to the spectacular spectral theory, which is the key to answering all of these questions.

  Using linear algebra to understand knots

  Cynthia Curtis, Professor of Mathematics at The College of New Jersey – Union College Class of 1987

  Thursday, February 14th, 1:00pm, Bailey 207, with reception at 12:30pm in Bailey 204

  Knots are prevalent in nature, and the study of knotting is important in diverse areas such as DNA, bonding of molecules, and statistical mechanics. Understanding knots has been fundamental within mathematics to our ability to understand three-dimensional spaces. In this talk we use linear algebra to generate polynomials, which help decide whether two given knots are different. This is a surprisingly hard question! The polynomials can also help us know when to look for hidden symmetries in the knots. The first knot polynomial we introduce was found by James Waddell Alexander II in 1923. We then discuss new polynomials arising from research with undergraduates Vincent Longo, Alyssa Springstead, and Hoang Cao at The College of New Jersey.

  Generalizing composition of functions and Operads

  Peter Bonventre, Union College Class of 2011

  Friday, February 8th, 1:00pm, Bailey 207, with reception at 12:30pm in Bailey 204

  Given two single-variable functions, we are allowed to take their composite to produce a new function again of a single variable. In this talk, we will ask: “In what other contexts does ‘composition of functions’ make sense?”. We will slowly broaden our definitions of “function” and “composition”, starting with the types of functions that appear in the Calculus sequence, and moving to include well-behaved geometric figures. This will lead us to the abstract concept of an operad. We will give several examples, as well as an interpretation of what these new objects can do for us.

  The Joy of Abstraction

  Kimmo Rosenthal, Union College

  Thursday, January 31st, 1:00pm, Bailey 207, with reception at 12:30pm in Bailey 204

  The imagination is the only genius. It is intrepid and eager and the extreme of its achievement lies in abstraction Wallace Stevens.

  It may seem incongruous for the epigraph to a math talk to be from one of the great American poets. However, while the ubiquity and utility of mathematics is widely acknowledged, its burnish of aestheticism is much less so. Can the old dictum “art for art’s sake” be replaced by “math for math’s sake”? In this day and age, when relevance, applicability, and connections with other disciplines are touted as paramount, is there still a place for purely abstract mathematics viewed more as an intellectual art form? Abstraction has always appealed to me and indeed guided me. Why does it often provoke outright hostility? We shall follow the path of abstraction from the set theory of Cantor (called a “corrupter of youth”) to point-set topology, followed by the mysterious emergence of Bourbaki (the mathematician who never existed), and finally category theory, which earned the epithet of “abstract nonsense”. Of course, there will be some mathematics along the way, reasonably modest in scope.

  Hall’s Marriage Theorem

  Alan Taylor, Union College

  Thursday, January 24th, 1:00pm, Bailey 207, with reception at 12:30pm in Bailey 204

  Suppose we have a collection of women and a collection of men, and each woman finds some of the men acceptable (and the rest not). When is it possible to match each woman with a man she considers acceptable, subject to the obvious constraint that the matching be one to one? The answer to this metaphorical question is a beautiful result in finite combinatorics known as Hall’s marriage theorem. We will discuss Hall’s theorem, sketch a proof of it, and consider a couple of natural questions it suggests, all with the hope of providing an illustration of how research gets done in mathematics.

  Summer Opportunities for Math Students

  Thursday, January 17th, 1:00pm, Bailey 207, with reception at 12:30pm in Bailey 204

  This week’s seminar will focus on ways in which you can put your mathematical skills to use over the summer.

  Julia Greene ’19 will speak about the Teaching Experiences for Undergraduates Program, Professor Jeff Hatley will speak about Research Experiences for Undergraduates, and Keri Willis of the Becker Career Center will speak about summer internships.

• Fall 2018

  Turning the lights out, mathematician style

  Leila Khatami, Union College

  Thursday, November 1st, 1:00pm, Bailey 207, with reception at 12:30pm in Bailey 204

  “LIGHTS OUT!” is a single player game played on a 5 by 5 grid where each cell has a button that can be turned on or off. Pressing a button toggles the light in the cell and its neighboring cells. The game starts with some cells turned on and some turned off. The goal of the game is to turn all cells off. The game was originally introduced in 1995 as a handheld electronic came. Nowadays, the original game, as well as many of its variants, are readily accessible in app stores and elsewhere. It is not obvious (or even true!) that all starting configurations of the game are “solvable”. In this talk, we use mathematical tools to see if a game is “solvable”. We also briefly discuss ways to find the most efficient solutions for solvable games.

  Solving the General Cubic Equation

  ax3ax3+bx2bx2+cx+d=0cx+d=0

  Paul Friedman, Union College

  Thursday, October 25th, 1:00pm, Bailey 207, with reception at 12:30pm in Bailey 204

  The solution to the general quadratic equation,

  ax2+bx+c=0ax2+bx+c=0,

  is well-known to most high school students:

  

  
  It was also known to many “ancient” cultures … some dating back to 2000 BC! However, the solution to the general cubic equation, ax3+bx2+cx+d=0ax3+bx2+cx+d=0, is not as well known, and it was not found until the 1500s.

  In this talk, we will look at how the Renaissance mathematicians Scipione del Ferro, Tartaglia, and Cardano, solved the cubic equation, though we will do so using modern language and notation. As a cute consequence, we will be able to derive some remarkable identities, such as:

  

  Fair Division of a Graph: Envy Freeness up to one Good, or Two

  William Zwicker, Union College

  Thursday, Oct 18th, 1:00pm, Bailey 207, with reception at 12:30pm in Bailey 204

  Countries A and B are dividing up a disputed island with several cities, linked by roads:

  • • Each city must go entirely to A, or entirely to B
    • A city may be worth more to one country than to the other
    • You must be able to drive among A’s cities without going through B’s

  Can cities be allocated in a way that leaves neither country jealous of the other’s share?

  

  No – not in general. But with certain road networks one can always get within one city of this ideal. Which networks are these? With more than 2 countries, the question gets harder . . . in interesting ways.

  In its “classical” setting Fair Division concerns sharing a single, continuously divisible resource. Some solutions can be adapted to this new setting, but a lot needs to change.

  Forms of Remigration – Émigré Jewish Mathematicians and Germany in the Immediate Post-War Period

  Volker Remmert, , of the Bergische Universitat Wuppertal

  Tuesday, Oct 9th, 4:45pm, Bailey 207, with reception at 4:15pm in Bailey 204

  Over the last twenty years or so there has been a steady flow of historical studies on remigration into Germany in the immediate post-war period. These studies have described three main forms of academic remigration to Germany after World War II:

  1) returning to universities in Germany on a permanent basis as university professors;

  2) returning as visiting professors, assessing Germany without any obligation to stay;

  3) returning for guest lectures and academic visits.

  In this context my interest is in Jewish émigré mathematicians and their stance to Germany in the immediate post-war period.

  Math, Music, and Health Science

  Danielle Gregg ’19 and Robert Righi ’19, Union College Undergraduates

  Thursday, Oct 4th, 1:00pm, Bailey 207

  Much recent research has focused on discerning topological and geometric features of data. For example, by observing the “birth” and “death” of holes via an algebraic method known as persistent homology, we can distinguish noise from significant features in data. In analyzing the “shape” of data our research diverges into two separate fields: music and health science. How can one use geometric and topological methods to classify a variety of degenerative diseases of the eye or compare songs within an artist’s discography? Come learn about what two Union students researched over the past summer as well as the often non-linear research process.

  Action Graphs and Catalan Numbers

  Julie Bergner, University of Virginia and Cornell University

  Thursday, Sept 27th, 1:00pm, Bailey 207

  The Catalan numbers are given by a recursively-defined sequence and arise from over 200 different kinds of combinatorial objects. In 2013, two of my undergraduate research students, Gerardo Alvarez and Ruben Lopez, showed that a family of directed graphs called action graphs gives a new way to obtain this sequence. Since these graphs are defined inductively, one might ask what sequences we can get by using a different initial graph but the same induction process. Last year, three more students, Cedric Harper, Ryan Keller, and Mathilde Rosi-Marshall, looked into this question. They found new families, called kk-initial action graphs, which produce self-convolutions of the Catalan sequence. In this talk we’ll introduce the sequences and graphs involved and talk about how these comparisons were made.

  Cutting Up Space: Hilbert’s Third Problem and the Dehn Invariant

  Jonathan Campbell, Vanderbilt University

  Friday, Sept 21st, 1:00pm, Bailey 207

  Give two polyhedra of equal volume, can you cut up one into a finite number of pieces, and reassemble it into the other? This was a problem posed by Hilbert in a famous address. I’ll go through the two dimensional analogue of this problem, and present Dehn’s beautiful solution to Hilbert’s question. Time permitting, I’ll give some hint of how this easily stated problem shows up in my own research.

  Counting sudokus

  Professor Brenda Johnson, Union College

  Thursday, Sept 13th, 1:00pm, Bailey 207

  Sudoku is a popular puzzle involving a 9×9 grid in which one has to arrange the numbers 1 through 9 so that each row, column, and block contains all nine numbers. There are many interesting mathematical questions involving sudoku puzzles. In this talk, we’ll focus on a couple of questions related to counting sudokus. After discussing how many possible solutions there are for 9×9 and 4×4 sudokus, we’ll look at ways in which one can generate new sudokus from old ones, and whether or not these techniques can be used to generate all sudokus of a given size.